Factorial is a mathematical term that is the product of all preceding numbers like the factorial of “7” will be “7 * 6 * 5 * 4 * 3 * 2 * 1”. It is used in major mathematical concepts like algebra, probability, data sets, etc. The purpose of its utilization in computer science is to find out all possible options or outcomes for specific tasks. It is symbolically represented by the “!” sign. There are various approaches to calculating the factorial and the “recursion” is one of them.
This guide deals with finding a factorial of a provided number using the recursion approach in Java.
How to Find Factorial of a Number Via Recursion in Java?
As already discussed, the “Recursion” is one of the approaches for finding the “Factorial” of a number. This approach calls itself again and again till the base condition is satisfied. In our case, the recursive function starts from the provided “number” and multiplies it with the preceding numbers. After each call, the value of a provided number is decreased by a factor of “1”. For instance, consider the below code:
public class factorializations{
public static long recursiveFact( long num )
{
if ( num <= 1 ) {
return 1;
}
else {
long numFact = num * recursiveFact( num - 1 );
System.out.println("Factorial of Included Number: " + num + " is -> " + numFact);
return numFact;
}
}
static public void main(String[] args)
{
long result = recursiveFact( 6 );
System.out.println("\nThe Factorial of Provided Number '6' is => " + result);
}
}This Java code:
- First, create a custom “recursiveFact()” function accepting a single parameter “num”.
- Inside it, utilize the “if/else” conditional statements. The “if” statement returns “1” whenever the value of the “num” parameter is less than or equal to “1” and breaks the execution cycle.
- In the else part, call the “recursiveFact()” function having the parameter of “num -1” and multiply the returned value with the “num” variable.
- This generates a factorial of the preceding number and stores the result in a variable named “numFact”.
- Finally, invoke the “recursiveFact()” method with the parameter of a targeted value whose factorial needs to be found.
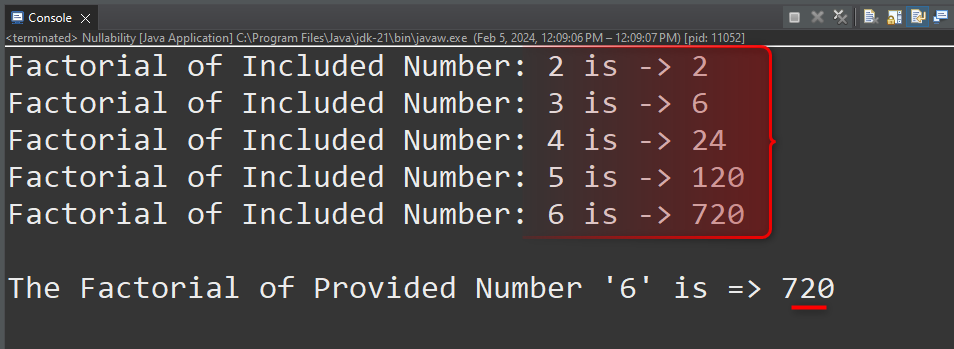
The output confirms that the factorial of a provided value is displayed along with the factorial of all preceding values:
How to Find Factorial of a Number Using Tail Recursion in Java?
The “Tail Recursion” is another type of recursion that is considered a better alternative approach due to its optimization. In the “Tail” recursion, the last statement of an entire code is executed when there is nothing left to execute after the recursion call. It is optimized by the compiler because the stack depth to execute in case of tail recursion is much less than the original recursion.
Let’s proceed to find the factorial of the provided number using recursion:
public class factorializations{
static int tailFact(int n, int x)
{
if (n <= 0)
{
return x;
}
return tailFact(n - 1, n * x);
}
static public void main(String[] args)
{
System.out.println("The factorial Using Tail Recursion for '6' is =>" + tailFact(6, 1));
}
}The internal working of the above code is as follows:
- First, create a function “tailFact()” with two parameters: “n” and “x” storing the targeted value and initial point.
- In this function, return the value of “x” if the value of a provided number is smaller or equal to “0”. Also, invoke the “tailFact()” function with the parameters of “n-1” and “n*x” to find the factorial recursively for each preceding number.
- Finally, invoke the “tailFact()” method and pass the targeted and initial stages as the first and second arguments.
Output

That’s all about calculating the factorial of a number recursively in Java.
Conclusion
To find the factorial of a number using “recursion”, multiply the provided number by all preceding numbers recursively. In recursive calling the method is called with different parameters inside the same method definition part. Another approach is using the “Tail recursion” which is another type of recursion. The main difference is that it is placed at the end of a function mostly with the return statement because there should be no code after the calling of the function for the tail recursion.
